CALCULADORA DE PRODUTOS MATRICIAIS


As matrizes são definidas como um conjunto ordenado de caracteres, que são distribuídos em linhas e colunas. Suas aplicações são destinadas a diversos setores do estudo, facilitando e organizando diversas situações. Entre as áreas que utilizam este recurso estão a Economia, Engenharia, Matemática, Física, dentre outras.
As aplicações das matrizes podem ser tabelares, mas também podem ser destinadas a conceitos ainda mais matemáticos. A utilização deste artifício é bastante empregada nas matérias de cálculo e física do ensino superior dos cursos que trabalham com diciplinas de exatas em geral (as engenharias são um bom exemplo). Desta maneira, os conceitos de produto escalar, produto vetorial e produto misto são bem importantes de serem entendidos no contexto matricial, pois a partir deste conhecimento poderemos realizar diversos cálculos e resolver inúmeros problemas relacionando matrizes e vetores.
Quando são mencionadas operações matemáticas envolvendo matrizes e suas aplicações é necessário que a noção intuitiva e literária de vetores esteja bem situada. Um vetor se caracteriza por ser um segmento de reta, orientado, responsável pela caraterização das grandezas definidas como vetoriais, empregando assim módulo, direção e sentido onde está inserido (Imagem 01).
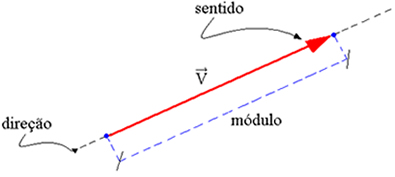
Imagem 01: Representação de um vetor e suas indicações.
A operação entre dois vetores que resulta em um número é denominado produto escalar ou produto interno. Utilizando dois vetores, A e B, o produto escalar entre eles pode ser definido como a multiplicação do módulo de A pelo módulo de B e pelo cosseno do menor ângulo entre os dois, observe abaixo (Equação 01):

Equação 01
A representação simbólica do produto escalar é um "ponto" (.) que o diferencia do produto vetorial por exemplo que utiliza a simbologia do "vezes"(x). O produto interno também pode ser calculado em representação canônica da seguinte maneira (Equação 02):
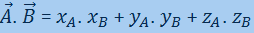
Equação 02
É interessante considerar que o ângulo que os vetetores então situados entre si influenciará no valor final do produto interno. Considerando θ a angulação entre os vetores A e B, se θ menor 90º formasse um ângulo agudo de componete positiva, já se θ maior 90º o ângulo é obtuso e o resultado é negativo (Imagem 02).
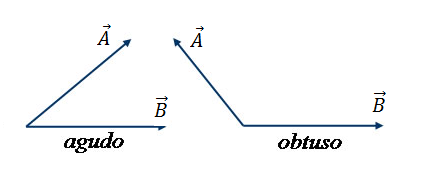
Imagem 02
Considere A, B e U vetores e K uma escalar:
A.B = B.A
A.A =|A|.|A| = A²
U(A.B) = U.A + U.B
(KA).B = A.(K.B) = K.(A.B)
|K.A| = |K|.|A|
|U.A| = |U|.|A| (desigualdade de Schwarz)
|U+A| = |U|+|A| (desigualdade triangular)
Talvez a utilização mais comum do produto escalar seja na mecânica, para calcular o trabalho realizado por uma força que age em um determinado deslocamento (Equação 03). Ademais, outro exemplo aplicado seria em eletromagnetismo para calcular o fluxo magnético que percorre uma superfície (Equação 04).
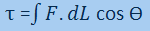
Equação 03
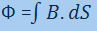
Equação 04
O produto Vetorial é a operação matemática que a partir de vetores primários gera-se um vetor final. Um vetor A e um vetor B geraram um terceiro vetor C perpendicular tanto a A quanto a B, ou seja, dois vetores gerando um terceiro de modo que o ângulo entre eles em relação ao vetor resultante é de 90 graus (Imagem 03). Referencialmente a representação do produto vetorial é dada por “x” entre os vetores calculados (AxB), lendo-se “A vetorial B”.
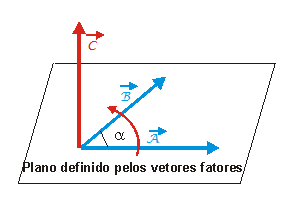
Imagem 03: Vetores fatores são os vetores que vão gerar o vetor C, observe o ângulo formado entre os vetores A e C e também B e C (90 graus).
A resolução do produto vetorial requer mais passos que o do produto interno. Pode-se usar o principio do cálculo do determinante (obedecendo as direções vetoriais) que é feito de diversas fórmulas, ficando a critério pessoal, no exemplo abaixo foi usado o método de Sarrus (Imagem 04).

Imagem 04: Exemplificação de uma das formas de calcular produto vetorial pelo método de Sarrus.
Como já foi mencionado o produto vetorial entre dois vetores resulta em um terceiro vetor e o módulo dele pode ser definido como sendo igual ao produto dos módulos de A e B, e o seno do menor ângulo entre eles (Equação 05).

Equação 05: fórmula do módulo do produto vetorial,onde o "n" é o vetor perpendicular tanto a A quanto a B, e na maior parte das vezes não é usual.
É interessante salientar que a ordem dos vetores calculados no produto vetorial influência na direção do vetor resultante, não sendo assim um cálculo de ordem comutativa (a exemplo de prova esta a primeira propriedade citada logo abaixo). Deve-se observar também a ordem em que os vetores estão sendo dirigidos, se forem no sentido horário a orientação é positiva se forem no sentido anti-horário negativa.
Considere A, B e U vetores e K uma escalar:
A x B = - (B x A)
(k.B) x A = B x (k.A) = k (B x A)
A x (B+U) = A x B + A x U
O produto vetorial pode ser usado para substituir a regra da mão direita, familiar a todos os engenheiros que utilizam conceitos do eletromagnetismo em sua grade curricular. Considerando a mesma direção da força que age em um condutor de comprimento (L) e o fluxo de corrente(I), juntamente com a densidade de fluxo magnético (B), pode-se descrever a força magnética como um produto vetorial, expresso na Equação 06.
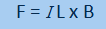
Equação 06
O produto misto ou produto triplo nada mais é que a combinação do produto vetorial e escalar entre três vetores que resultara em uma escalar (Equação 07), também chamada de determinante.
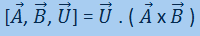
Equação 07
A expressão cartesiana do produto misto pode ser calculada utilizando os conceitos de produto vetorial e escalar, sendo mais proveitoso o cálculo do determinate de uma 3x3 já que se torna mais rápido e fácil, como mostra a imagem 05.

Imagem 05: utilização do produto escalar e vetorial para desenvolvimento do cálculo do produto misto em comparação com a informação que o mesmo também pode ser calculado por determinante da matriz que os vetores fomariam.
Considere A, B, U E W vetores e K uma escalar:
[A,B,U] = 0 - se um deles for o vetor nulo ou se os vetores são coplanares.
[A,B,U] = - [B,A,U] = [B,U,A]...
[A + W,B,U] = [A,B,U] + [W,B,U]
[K.A,B,U] = K.[A,B,U]
O produto triplo é muito utilizado nos nas matérias de exatas relacionadas a cálculo do ensino superior. Já que essa operação matemática define facilmente o volume de paralelepípedos e tetraedros (Imagem 06) em problemas que utilizam dimensões de vetores por exemplo.
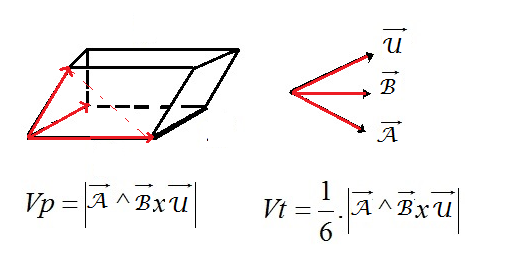
Imagem 06: A imagem acima mostra tanto a formula do volume do paralelepípedo (Vp), quanto a tetraedro (Vt), que vale 1/6 do volume total do paralelepípedo.
Produto Escalar e Vetorial
Produto Misto
Produto Escalar e Vetorial
Produto Misto